一、单次假设检验
假设我们收集了一批男生和女生的身高数据,想要研究的问题是总体上男生和女生的平均身高是否存在差异。如果我们计算当前样本里的男女身高均值的差异,那么这个差异一般不会为0,但是我们没有把握这个差异是否意味着男女在身高均值上存在差异,因为很有可能这个差异是由于随机抽样带来的偶然的差异(也许换一批样本差异就完全不同了)。为了解决这个问题,我们可以重复这个过程许多次(比如1000次),即采集1000批身高数据,然后在每批数据中计算男女平均身高的差异,这样我们就得到了1000个男女身高的均值差异,即我们得到了一个均值差异的分布(称作均值差异的抽样分布,sampling distribution of the difference between means)。有了抽样分布,我们就知道了男女身高的均值差异在不同样本中是如何变化的。如果在绝大多数样本中,男女身高的均值差异都是大于0的(或者小于0),那么我们就比较有信心总体上男女平均身高存在差异。如果有一半的样本是男生身高均值大于女生身高均值,另一半样本是男生身高均值小于女生身高均值,那么我们就没有信心总体上男女身高均值存在差异。
在实际研究中,我们往往只有一批数据,并且不可能重复采集1000批数据,但是我们可以在只有一批数据的情况下获得均值差异的抽样分布。在满足一定假设的情况下(比如,男女身高总体是正态分布),均值差异的抽样分布是T分布(或者正态分布)。在假设男女身高均值没有差异的情况下(零假设,null hypothesis),我们可以计算出观察到等于或者大于当前T值(的绝对值)的概率,这个概率就是P值。P值表达的意思就是,如果零假设为真,我们有多大概率能够得到当前样本的差异(甚至更大的差异),如果这个概率很小,那么可能零假设是有问题的,我们就拒绝零假设,认为男女身高均值是存在(显著)差异的。一般显著性水平设置为0.05,即如果P值小于0.05,就认为差异显著。另一方面,当零假设为真的时候,虽然我们观察到当前样本的差异的概率很小,但是还是有可能的,如果我们拒绝了零假设,那么就犯了第一类错误(Type-I Error),也叫做假阳性(False Positive)。第一类错误的概率(Type-I Error Rate)是当零假设为真但是拒绝了零假设的概率,比如这个研究被重复了1000次,如果显著性水平为0.05,在零假设为真的情况下,1000次研究里大约有%5的研究会出现第一类错误。在上面这个过程中,我们需要假设男女身高总体分布是正态分布才能知道均值差异的抽样分布的形式,这种方法通常称为参数检验(parametric test)。除了参数检验,我们也可以使用非参数检验(non-parametric test),常见的包括自助法(bootstrap)和置换检验(permutation test)。比如,自助法通过对当前仅有的样本进行重复抽样,也可以得到对于均值差异的抽样分布的近似估计。非参数检验并非没有引入假设,只是一般比参数检验的假设要更少或者更弱。无论是使用参数检验还是非参数检验,我们对于P值和第一类错误的概率的解读是一样的。
二、多次假设检验
假设对于当前样本除了采集了身高数据,还采集了体重、智力、反应时等等很多指标,如果我们对每个指标都进行组间比较,那么我们就同时做了多次假设检验(称作多重比较,multiple comparison)。整体错误率(Family-wise Error Rate, FWER)表示多次假设检验中至少有一次检验出现假阳性(即零假设为真,但拒绝了零假设)的概率。如果多次假设检验相互之间是独立的,那么FWER=1-(1-a)^m,其中a表示单次假设检验中采用的显著性水平,m表示假设检验的次数。假设a=0.05,m=10,那么FWER=0.40,也就是说如果我们同时做了10次假设检验,那么其中至少出现一次假阳性的概率为40%。为了控制由于多重比较导致的整体错误率升高(相比于单次比较而言),一种简单的方法是使用Bonferroni校正(Bonferroni correction)。比如,要保证FWER最多为0.05,Bonferroni校正要求在多重比较中,单个假设检验的显著性水平为0.05/m,如果m=10,那么单个假设检验的显著性水平应为a=0.005。除了FWER,错误发现率(False Discovery Rate, FDR)是另一种度量多重比较中假阳性概率的方法。假设在m次假设检验中,在R次中拒绝了零假设(称为发现,discovery),其中有V次是假阳性(称为错误发现,false discovery),Q=V/R表示当前错误发现的比例,那么FDR=E(Q),即FDR表示错误发现比例的期望值,E表示期望。控制FDR最常用的方法是Benjamini-Hochberg校正(BH correction)。以一个例子来说明我们对于FWE或者FDR校正后的结果的解读的区别,我们比较了男女在100个不同指标上的差异,如果在控制FWER=0.05的情况下,得到20个显著的差异,那么我们倾向于认为这20个差异都不是假阳性(或者像单次检验一样去解读多次检验中每次检验的结果);如果在控制FDR=0.05的情况下,得到20个显著的差异,那么我们倾向于认为大约有1个差异是假阳性(20*0.05=1)。
一个问题是,哪些假设检验应该当做一个整体(family)?在脑成像研究中,如果我们对图像中的每个体素分别进行假设检验,那么这些检验是需要当做一个整体进行多重比较校正的。如果我们不进行校正,或者校正方法有问题,那么假阳性的概率会大大增加。在Bennett et al. (2009)中,研究者对一条死鱼呈现了观点采择的任务并进行了fMRI扫描,如果单个体素的显著性水平设置为0.001,那么有16个体素显著或者在任务中“激活”了。这显然是不可能的。如果进行了FWE或者FDR校正(即控制了FWER或FDR为0.05),则没有显著的体素。在Eklund et al. (2016)中,研究者发现团块水平的校正方法(在某些情况下)实际的FWER可能高达20%(远高于预期的5%),而如果不进行校正,FWER高达70%。这篇研究在当时影响力很大,也说明正确进行多重比较校正是重要的。
三、脑成像中的多重比较校正思路
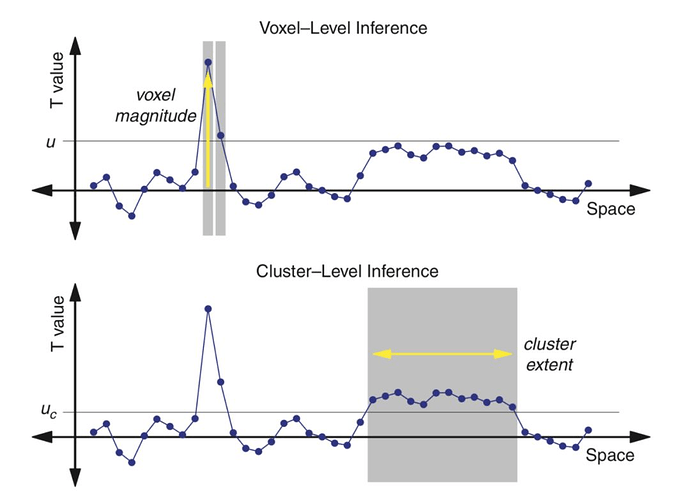
在脑成像中我们仍然可以用一般性的多重比较校正方法,比如上面提到的Bonferroni校正或Benjamini-Hochberg校正,但是这些方法往往过于保守,因为没有考虑到脑成像数据的特点。脑成像数据的一个特点是空间依赖性(spatial dependency),即相邻体素之间相关性是很强的。比如,虽然进行比较的体素个数可能有上万个(上万次假设检验),但是完全独立的假设检验数量要小得多。体素间相关性的一个来源是,虽然体素是图像的最小单元,但是不是脑活动的最小单元,很难想象只有一个体素在“活动”而周围体素毫无反应的情况。利用这种空间依赖性,脑成像中特有的多重比较校正方法可以分为体素水平(voxel-level inference)和团块水平(cluster-level inference)两种。体素水平的校正关注的是单个体素是否显著(在控制FWER的情况下),而团块水平的校正关注的是团块大小是否显著。在下图中,横轴表示体素,纵轴表示每个体素的T值,体素水平的校正检验的是单个体素的T值(或P值)是否高于阈值(假设这个阈值可以保证FWER不高于0.05),图中有两个体素显著;团块水平的校正首先需要设置一个形成团块的阈值(即图中的uc),图中有两个团块(一个包含12个体素,一个包含2个体素),然后检验团块的大小是否高于阈值(假设这个阈值可以保证FWER不高于0.05)。只有包含12个体素的团块是显著的,而在体素水平显著的两个体素所构成的团块并不显著。所以体素水平校正和团块水平校正的一个明显区别是,团块水平的校正需要设置两个阈值,第一个阈值用于形成团块(cluster-forming threshold)。
图片来源:Poldrack, R. A., Mumford, J. A., & Nichols, T. E. (2011). Handbook of functional MRI data analysis. Cambridge University Press.(第113页,图7.1)
那么如何确定这个阈值以保证FWER或者FDR不高于设定的水平(比如0.05)?我个人常用的方法有基于高斯随机场(Gaussian Random Field Theory, Friston et al., 1994)和置换检验(Nichols & Holmes, 2002)两种。比如,SPM和FSL提供了基于高斯随机场的校正工具,FSL和FreeSurfer都可以使用置换检验进行多重比较校正。此外,有一种流行的方法叫做基于TFCE的校正(TFCE-based inference,Smith & Nichols, 2009),虽然仍然是在体素水平进行检验,由于引入了TFCE统计量,使得体素水平也包含了团块的信息,可以看做是体素水平校正和团块水平校正的一种结合。
四、参考文献
-
Bennett, C. M., Miller, M. B., & Wolford, G. L. (2009). Neural correlates of interspecies perspective taking in the post-mortem Atlantic Salmon: An argument for multiple comparisons correction. Neuroimage, 47(Suppl 1), S125.
-
Eklund, A., Nichols, T. E., & Knutsson, H. (2016). Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proceedings of the national academy of sciences, 113(28), 7900-7905.
-
Friston, K. J., Worsley, K. J., Frackowiak, R. S., Mazziotta, J. C., & Evans, A. C. (1994). Assessing the significance of focal activations using their spatial extent. Human brain mapping, 1(3), 210-220.
-
Nichols, T. E., & Holmes, A. P. (2002). Nonparametric permutation tests for functional neuroimaging: a primer with examples. Human brain mapping, 15(1), 1-25.
-
Smith, S. M., & Nichols, T. E. (2009). Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage, 44(1), 83-98.
本人统计水平非常有限,不能对本文内容准确性负责,请谨慎参考,并欢迎讨论。
(本文部分内容最初于2019年发布在个人公众号上,这里重新进行了整理,并补充了一些内容。)