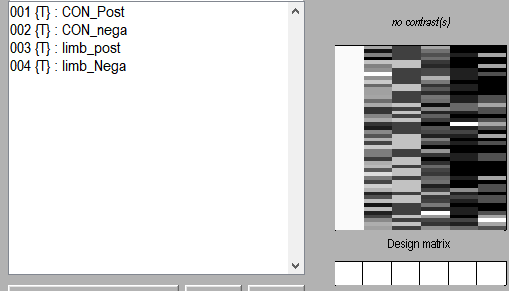
问题①
在用SPM做VBM时,我希望得到和我两个量表(A B)分数相关的脑区,但这两个量表的分数是有显著相关性的(spearman rho≈0.5,P《0.05),而且这种相关结合实际来看也是合理的。我尝试用SPSS中的共线性模型对我拟纳入的变量(age,sex,A,B)做共线性的诊断,发现其VIF值(<2)和容差(>0.6)都在可接受范围内(图1)。
1)那么当我希望得到与A量表相关的脑区时,我的设计应该是 age sex A B, 还是 age sex A呢?
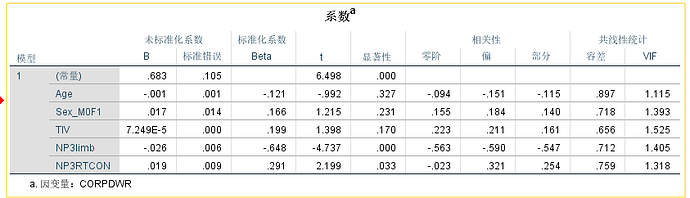
事实是当我把A B都covariate时和仅把A B 分别纳入模型时相比,具有相关性的脑区的位置是相同的,但其显著性有差异。当把 A B两个量表都纳入模型,也就是用 age sex A B的模型,0 0 0 0 1、、 0 0 0 1 0(Fig 2)的设计矩阵获得与 B量表正相关,A量表正相关的脑区时(图2),其差异可以通过多重校正。 而当用age sex A 及 0 0 0 1 获得A量表正相关脑区,age sex B 及 0 0 0 0 1获取B量表正相关的脑区时,其结果脑区不能通过多重校正。
2)另外,多重共线性的诊断是必须对符合LINE原则的自变量进行吗?
问题②
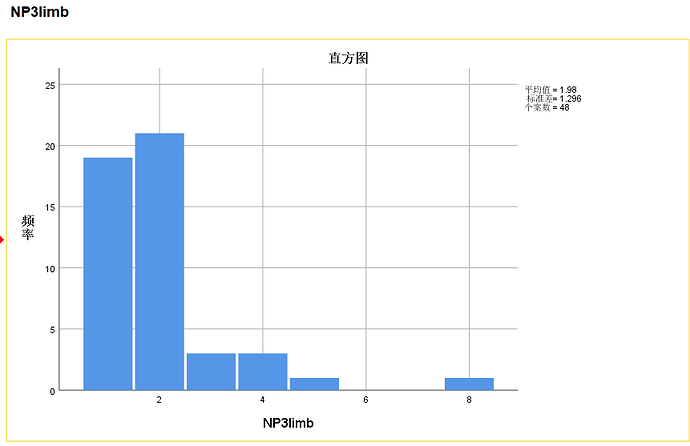
在SPM的GLM的模型中 我如果纳入的是 age sex A量表分数 3个covariate,我用fslstats将差异区的值提取出来,然后用SPSS 进行统计,我需要重现这种相关性,我想的是把 脑区的值 和 A量表分数分别作为GLM的因变量,将age sex作为自变量,将所得模型的残差做Pearson或spearman相关。对脑区的值利用这样的模型来求残差应该是合理的,因为脑区的值满足LINE原则。但A量表的分数是明显的偏态分布的数据,其似乎不满足LINE原则,这种情况下这样做还可以吗?